几何生成器模型

几何生成器模型#

在本教程中，我们将探讨实现在 networkx/generators/geometric.py 下的几何网络生成器模型，并将其应用于一个实际用例，以了解如何对这些模型进行参数化和使用。

导入包#

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx

几何/空间网络#

许多现实世界的复杂系统具有空间组成部分，这些组成部分限制了这些类型系统能够产生的网络结构。交通、电力和电信系统等基础设施网络、社交网络，甚至我们自身的突触网络，都嵌入在物理空间中。空间网络为具有空间元素的网络模型提供了一个框架，在这些模型中，节点嵌入在空间中，并包含一个度量，该度量决定了节点之间连接的条件。通常，连接的概率是度量的一个递减函数，大多数模型假设采用二维或三维欧氏距离。大多数空间网络模型的直觉是，距离越远的节点之间的连接成本越高，尽管可以建模任意的连接概率函数。

空间网络在如此广泛的现实世界系统中的潜在应用，激发了对这些网络的深入研究，提出了许多独特但密切相关的模型，并提供了许多网络属性的理论证明。Marc Barthélemy 在 2010 年撰写的《空间网络》评论文章 [1] 对该领域进行了全面概述，并回顾了最常见的空间网络模型的许多重要理论证明。在这里，我们将探讨 networkx 包中实现的一些最典型的空间网络模型。这些模型可以使用这些不同模型使用的仅三个模型参数进行分类：

  • \(R\) - 最大连接距离，即 networkx 中的 radius 参数

  • \(P(d_{ij})\) - 边连接概率作为距离 \(d_{ij}\) 的函数，其中 \(i \neq j\) 的节点 \(i, j\) 之间，即 networkx 中的 p_dist 参数

  • \(\theta\) - 节点权重连接阈值，即 networkx 中的 theta 参数

通常，节点均匀分布在单位正方形上，节点权重从某个权重分布中采样。距离 \(d_{ij}\) 通常假定为欧氏距离，但一些 networkx 模型允许自定义度量，而其他模型只允许 Minkowski 度量。

下图显示了通过共享参数化连接的空间网络模型之间的关系。

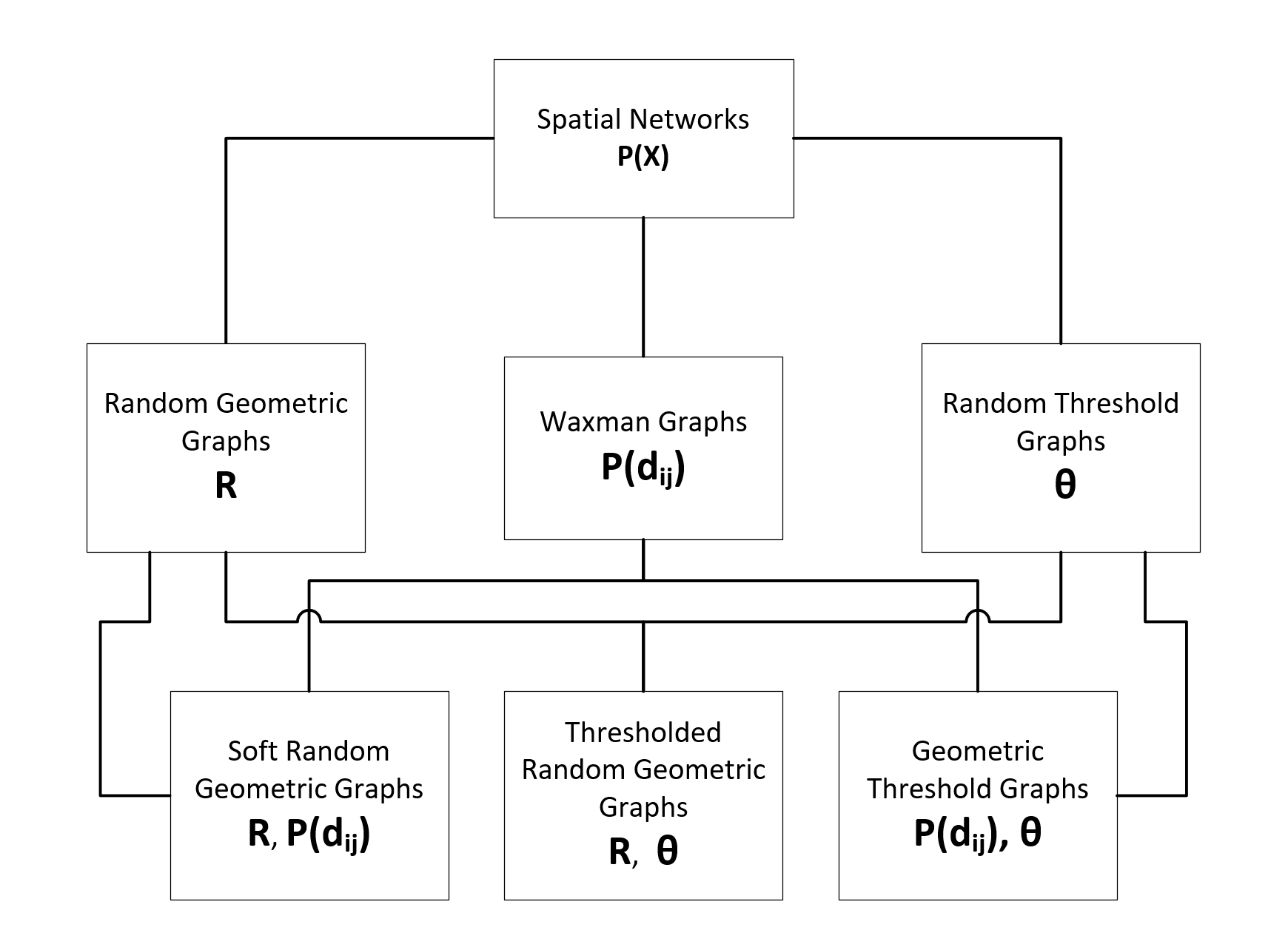
spatial_networks

各个模型的定义#

本节总结了各种模型。记号 \(E_{ij}\) 表示在节点 \(i\) 和 \(j\) 之间存在一条边。

随机几何图 (\(R\))#

d维随机几何图 (RGG) 是一种图，其中 \(N\) 个节点中的每一个都被分配在 \([0, 1]^{d}\) 框中的随机坐标，只有相互“接近”的节点通过边连接 [2]。任何在最大连接距离 \(R\) 内或等于 \(R\) 的节点都是连接的节点，并且网络的结构完全由 \(R\) 定义。RGGs 类似于单元盘图 [3]，已被广泛用于建模 Ad Hoc 无线网络。

\[ E_{ij}: d_{ij} \leq R \]

Waxman 图 (\(\alpha\))#

Waxman 图是 Erdős–Rényi 随机图的空间推广，其中节点的连接概率取决于它们之间距离的函数[4]。Waxman 提出的原始边概率函数在 \(d_{ij}\) 中呈指数形式，提供了两个连接概率调整参数，\(\alpha\) 和 \(\beta\)。

\[ P(d_{ij}) = \beta e^{\frac{-d_{ij}}{L \alpha}} \]

其中 \(L\) 是每对节点之间的最大距离。

边概率函数 \(P(d_{ij})\) 的形状在确定 Waxman 图的结构方面起着关键作用，但在现实世界网络中对 \(P(d_{ij})\) 的刻画似乎仍有争议。最常研究的函数族是上面的原始指数函数，或幂律函数 \(-{d_{ij}}^{-\alpha}\)。

\[ E_{ij} \propto P(d_{ij}) \]

阈值图 (\(\theta\))#

如果我们可以为顶点分配权重，使得一对不同的顶点当且仅当其分配权重的总和等于或超过指定阈值 \(\theta\) 时相邻，则简单图 G 是一个阈值图 [6]。阈值图本身不是空间网络，因为它们不包含特定的几何或度量，但它们引入了将节点权重作为网络模型一部分的能力，这被其他空间网络模型（例如几何阈值图）所利用。

\[ E_{ij}: (w_i + w_j) \geq \theta \]

地理阈值图 (\(P(d_{ij}), \theta\))#

地理阈值图是阈值图的地理推广，其中一对权重为 \(w_i, w_j\) 且距离为 \(d_{ij}\) 的顶点当且仅当权重 \(w_i\) 和 \(w_j\) 的总和与边连接函数 \(P(d_{ij})\) 的乘积大于或等于阈值 \(\theta\) 时连接。[8]

\[ E_{ij}: (w_i + w_j) P(d_{ij}) \geq \theta \]

软随机几何图 (\(R, P(d_{ij})\))#

随机几何图最近的一个扩展是将最大连接距离 \(R\) 内的节点之间的距离影响耦合进来，以便更好地建模现实世界系统，其中节点的接近度不一定保证“接近”节点之间的连接。在软随机几何图中，节点 \(i\) 和 \(j\) 之间的连接概率是它们距离 \(d_{ij}\) 的函数，如果 \(d_{ij} \leq R\)。否则，它们是断开的 [7]。

\[ E_{ij} \propto P(d_{ij}) \textrm{ if } d_{ij} \leq R \]

阈值随机几何图 (\(R, \theta\))#

阈值随机几何图扩展了 RGGs，将节点权重纳入模型中，其中连接只在具有足够高权重的节点之间建立，且限制在节点之间的最大连接距离以内 [9]。

\[ (w_i + w_j) \geq \theta \textrm{ if } d_{ij} \leq R \]

一个启发性的例子#

在本教程中，我们将使用特斯拉北美超级充电桩网络，以突出说明 networkx 中实现的各种空间网络模型如何进行参数化和使用。

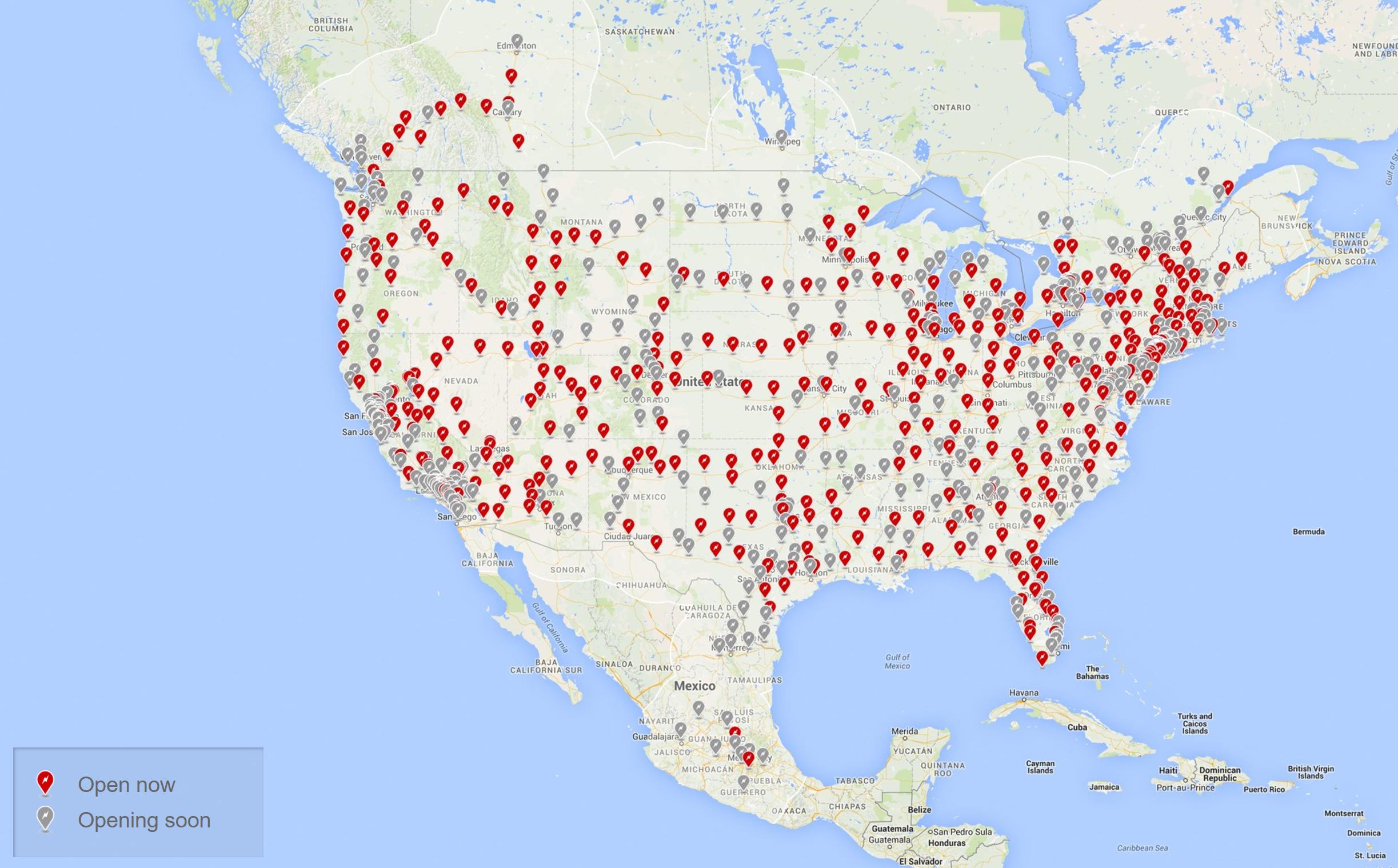
spatial_networks

超级充电桩数据来自 supercharger.info，过滤了加拿大和美国的超级充电桩位置，截至 2017 年 4 月共有 385 个已开放的超级充电桩。收集到的数据已被构建为 Networkx 图，该图由嵌套字典组成，以每个超级充电桩 GPS 坐标的 geohash 作为键，这些坐标已被转换为投射到单位正方形上的嵌入。节点权重是每个超级充电桩所在城市的总人口，占北美总人口的百分比。利用这个数据集，我们可以使用 networkx 中实现的各种空间网络来建模超级充电桩网络。

# Some matplotlib settings
mpl_params = {
    "axes.titlesize": 20,
    "figure.figsize": (12, 4),
}
plt.rcParams.update(mpl_params)

接下来，我们加载数据并构建图。

# from networkx.readwrite import json_graph
import json

# load json-ed networkx datafile
with open("data/tesla_network.json") as infile:
    G = nx.json_graph.node_link_graph(json.load(infile), edges="links")

print(G)

Graph with 385 nodes and 0 edges

# example node data structure keyed on geohash of GPS cords
G.nodes["dr7k46ycwwb8"]

{'SC_index': 173,
 'geohash': 'dr7k46ycwwb8',
 'weight': 0.00014093906625032375,
 'GPS_lon_lat': [-74.07126104459167, 41.49977498687804],
 'lat': 41.49977498687804,
 'lon': -74.07126104459167,
 'population': 28101,
 'pos': [0.8123107474668945, 0.42622282744786055],
 'GPS': [41.49977498687804, -74.07126104459167]}

# extract pos and weight attributes for use in models
nodes = G.nodes()
pos = nx.get_node_attributes(G, "pos")
weight = nx.get_node_attributes(G, "weight")

由于我们将可视化很多图，我们定义一些通用的绘图选项以获得一致的可视化效果。

node_opts = {"node_size": 50, "node_color": "r", "alpha": 0.4}
edge_opts = {"edge_color": "k"}

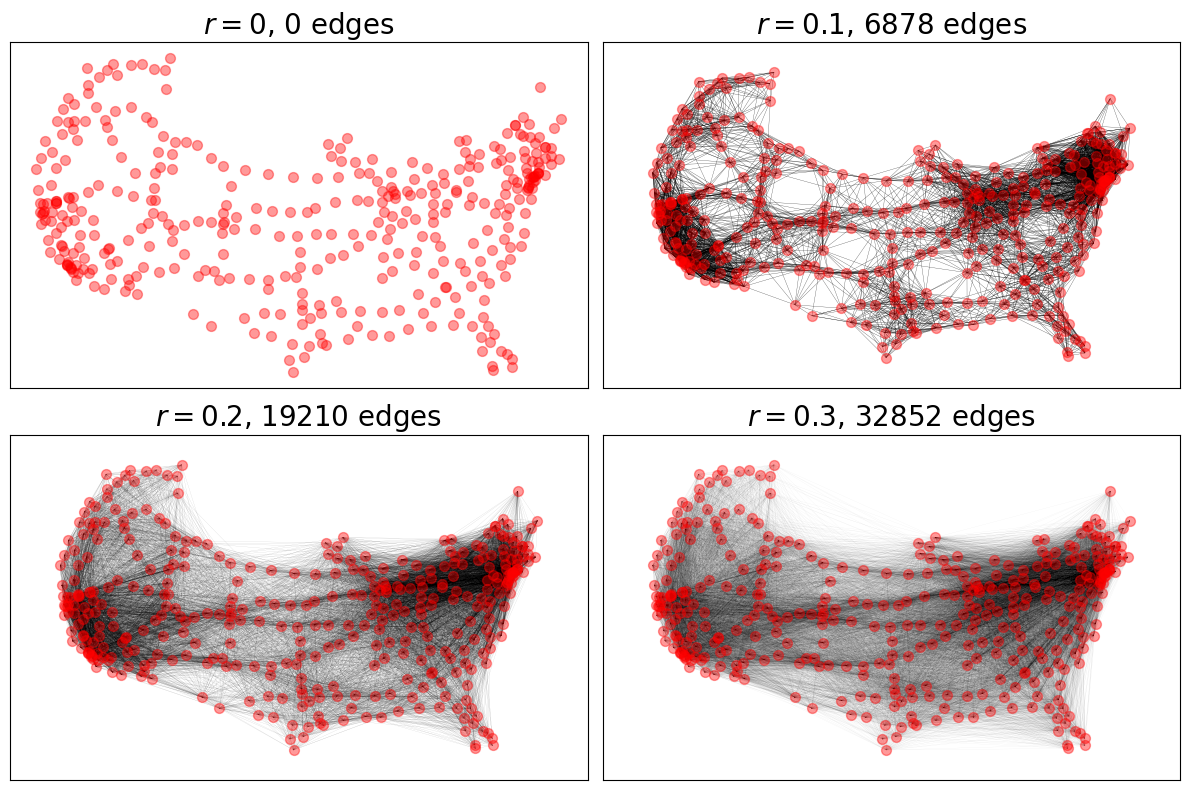
随机几何图#

对于 RGGs，我们看到增加最大连接距离参数 radius 对增加连接数量的影响。

fig, axes = plt.subplots(2, 2, figsize=(12, 8))
# Params for visualizing edges
alphas = (0.8, 0.8, 0.3, 0.1)
linewidths = (0.2, 0.2, 0.1, 0.1)

radii = (0, 0.1, 0.2, 0.3)
for r, ax, alpha, lw in zip(radii, axes.ravel(), alphas, linewidths):
    RGG = nx.random_geometric_graph(nodes, radius=r, pos=pos)
    nx.draw_networkx_nodes(G, pos=pos, ax=ax, **node_opts)
    nx.draw_networkx_edges(RGG, pos=pos, ax=ax, alpha=alpha, width=lw, **edge_opts)
    ax.set_title(f"$r = {r}$, {RGG.number_of_edges()} edges")
fig.tight_layout()
../../_images/c90379b31661ecab0475323e0c939c61c41612d4d4ff185ca06cfae40d226afa.png 
# Make edge visualization more prominent (and consistent) for the following
# examples
edge_opts["alpha"] = 0.8
edge_opts["width"] = 0.2

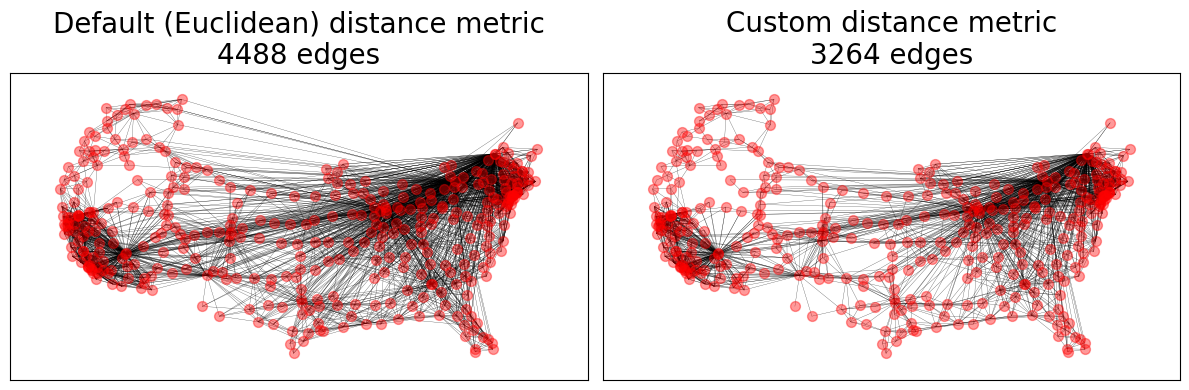
地理阈值图#

GTG 模型允许广泛的自定义参数，包括自定义节点位置、权重以及节点之间的度量和连接概率 \(P(d_{ij})\)。默认的 \(P(d_{ij})\) 模型是两个连接节点的度量值 \(r\) 的 \(-\alpha\) 次幂，其中 \(\alpha\) 参数的默认值为 2。

fig, axes = plt.subplots(1, 2)

# Custom distance metric
dist = lambda x, y: sum(abs(a - b) for a, b in zip(x, y))

distance_metrics = {
    "Default (Euclidean) distance metric": None,  # Euclidean distance
    "Custom distance metric": dist,
}

for (name, metric), ax in zip(distance_metrics.items(), axes.ravel()):
    GTG = nx.geographical_threshold_graph(
        nodes, 0.1, pos=pos, weight=weight, metric=metric
    )
    nx.draw_networkx_nodes(G, pos=pos, ax=ax, **node_opts)
    nx.draw_networkx_edges(GTG, pos=pos, ax=ax, **edge_opts)
    ax.set_title(f"{name}\n{GTG.number_of_edges()} edges")
fig.tight_layout()
../../_images/ca4be908006d93a6c5bcf0a2c72df40f377341b51c805b48f1582d3ebc41d4cd.png 
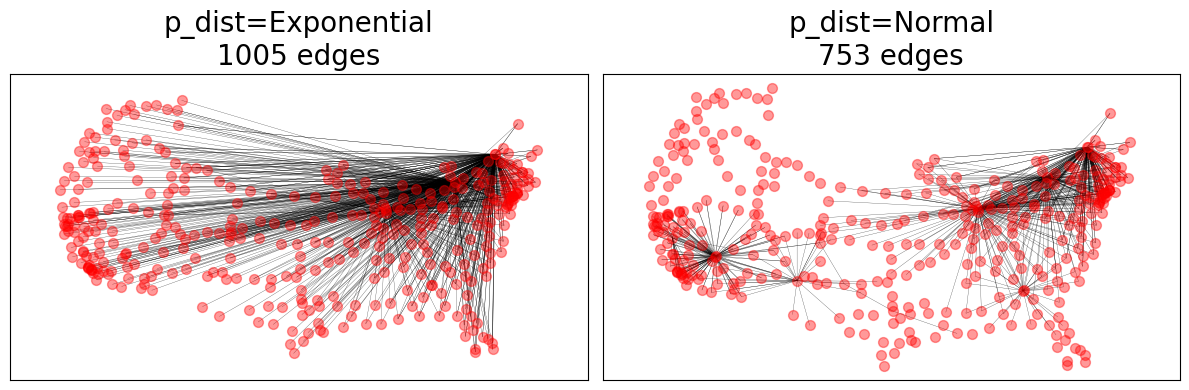
fig, axes = plt.subplots(1, 2)

# Evaluate different p_dists
import math
from scipy.stats import norm

p_dists = {
    "p_dist=Exponential": lambda d: math.exp(-d),
    "p_dist=Normal": norm(loc=0.1, scale=0.1).pdf,
}

for (name, p_dist), ax in zip(p_dists.items(), axes.ravel()):
    GTG = nx.geographical_threshold_graph(
        nodes, 0.01, pos=pos, weight=weight, metric=dist, p_dist=p_dist
    )
    nx.draw_networkx_nodes(G, pos=pos, ax=ax, **node_opts)
    nx.draw_networkx_edges(GTG, pos=pos, ax=ax, **edge_opts)
    ax.set_title(f"{name}\n{GTG.number_of_edges()} edges")
fig.tight_layout()
../../_images/e6d81b919b249f3d49d9340afdc06992ed52b56cd4aaa89a91bf0561a77384b9.png

软随机几何图#

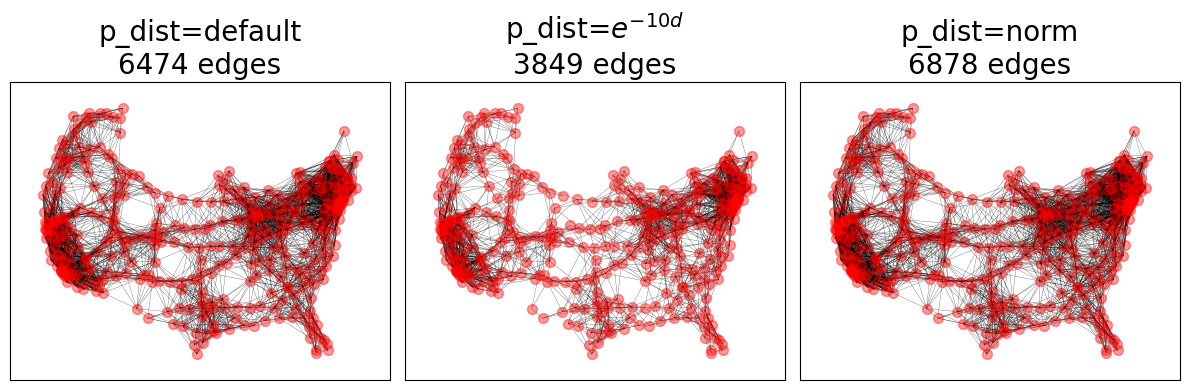
SRGGs 利用 RGGs 的最大连接距离参数 \(R\)，但提供了为最大连接距离内的节点输入任意连接概率函数 \(P(d_{ij})\) 的能力。networkx 中 SRGGs 的默认 \(P(d_{ij})\) 函数是一个指数分布，其速率参数为 lambda=1。

fig, axes = plt.subplots(1, 3)

pdfs = {
    "default": None,  # default: exponential distribution with `lambda=1`
    r"$e^{-10d}$": lambda d: math.exp(-10 * d),
    "norm": norm(loc=0.1, scale=0.1).pdf,
}
for (title, pdf), ax in zip(pdfs.items(), axes.ravel()):
    SRGG = nx.soft_random_geometric_graph(nodes, 0.1, pos=pos, p_dist=pdf)
    nx.draw_networkx_nodes(G, pos=pos, ax=ax, **node_opts)
    nx.draw_networkx_edges(SRGG, pos=pos, ax=ax, **edge_opts)
    ax.set_title(f"p_dist={title}\n{SRGG.number_of_edges()} edges")
fig.tight_layout()
../../_images/96fc59a8ad1dc6c1579e624182d3a9294a4ecc700440bad5ef453fd8f3f85473.png

阈值随机几何图#

TRGGs 允许最大连接距离参数和阈值参数的耦合。TRGG 的默认权重是从速率参数为 lambda=1 的指数分布中抽取的。

fig, axes = plt.subplots(1, 2)

# Increased threshold parameter, theta, reduces graph connectivity
thresholds = (0.0001, 0.001)
for thresh, ax in zip(thresholds, axes):
    TRGG = nx.thresholded_random_geometric_graph(
        nodes, 0.1, thresh, pos=pos, weight=weight
    )
    nx.draw_networkx_nodes(G, pos=pos, ax=ax, **node_opts)
    nx.draw_networkx_edges(TRGG, pos=pos, ax=ax, **edge_opts)
    ax.set_title(f"Threshold = {thresh}, {TRGG.number_of_edges()} edges")
fig.tight_layout()
../../_images/d24a493b388b2ddd657d24cea79927544b1968af9e1391317657609cdd785744.png

参考文献#

目录