最低共同祖先#
在本教程中,我们将探索 NetworkX 中最低共同祖先算法 [1] 的 Python 实现,代码位于 networkx/algorithms/lowest_common_ancestor.py。本 Notebook 要求读者熟悉 NetworkX API。如果您是 NetworkX 新手,可以先阅读入门教程。
导入包#
import matplotlib.pyplot as plt
import networkx as nx
from networkx.drawing.nx_agraph import graphviz_layout
from itertools import chain, count, combinations_with_replacement
定义#
在深入研究算法之前,让我们先回顾一下祖先节点和后代节点的概念。
祖先:给定一个有根树,从根节点到节点 \(v\) 的路径上的任何节点 \(u\) 都是 \(u\) 的祖先。
后代:节点的后代是该节点的子节点,或是该节点某个后代的子节点。
最低共同祖先:对于树中的两个节点 \(u\) 和 \(v\),最低共同祖先是同时是 \(u\) 和 \(v\) 的祖先中,层级最低(即最深)的节点。
示例#
通过示例来学习概念总是一个好主意。考虑以下进化树。我们将绘制一个有向版本,并定义祖先/后代关系。
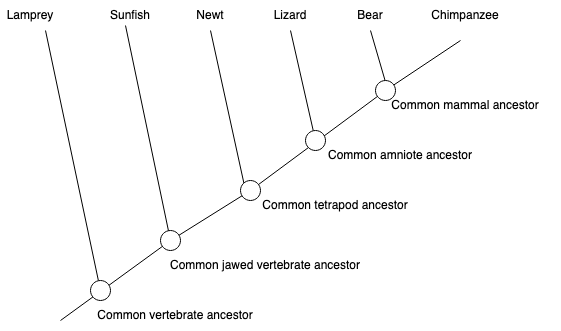
我们首先使用 NetworkX 绘制这棵树。
T = nx.DiGraph()
T.add_edges_from(
[
("Vertebrate", "Lamprey"),
("Vertebrate", "Jawed V."),
("Jawed V.", "Sunfish"),
("Jawed V.", "Tetrapod"),
("Tetrapod", "Newt"),
("Tetrapod", "Amniote"),
("Amniote", "Lizard"),
("Amniote", "Mammal"),
("Mammal", "Bear"),
("Mammal", "Chimpanzee"),
]
)
pos = graphviz_layout(T, prog="dot")
plt.figure(3, figsize=(16, 6))
nx.draw(
T,
pos,
with_labels=True,
node_size=4000,
node_color="brown",
font_size=11,
font_color="White",
)
plt.show()
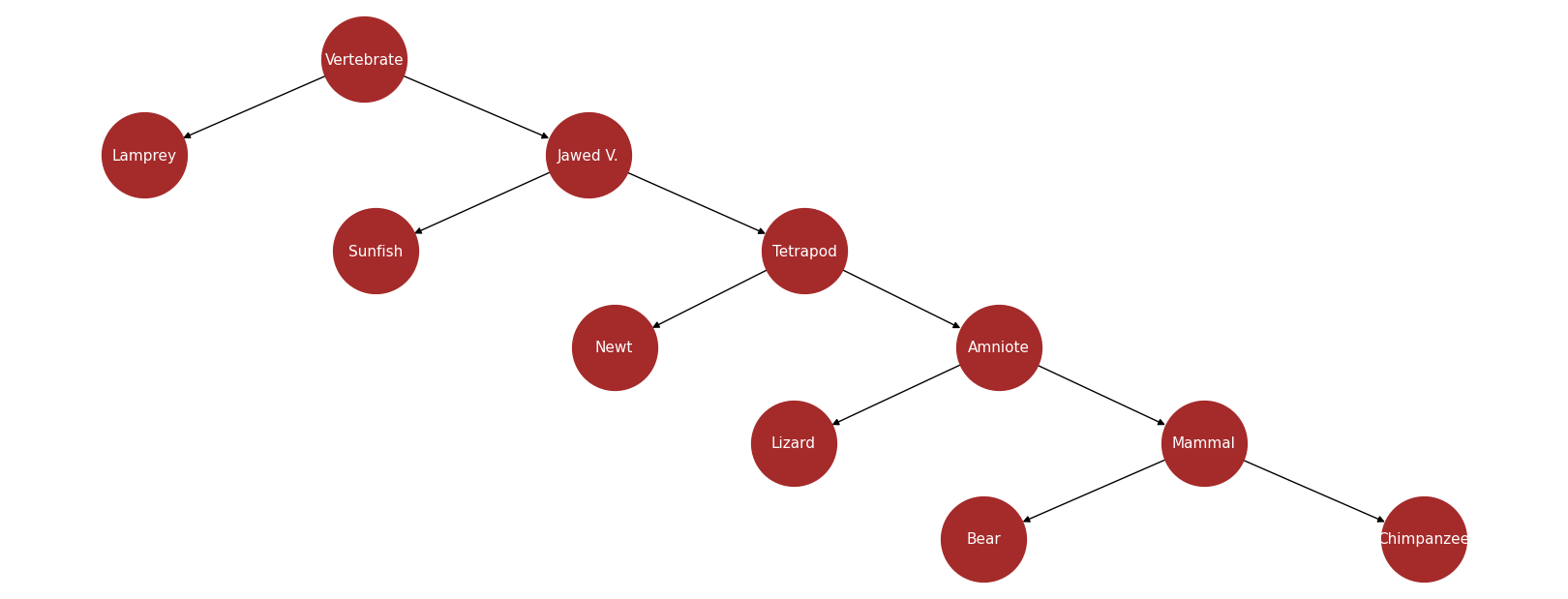
考虑上面的树,观察以下关系
节点 Mammal 的祖先
为此,我们将沿着从根到节点 Mammal 的路径。
节点 Vertebrate, Jawed Vertebrate, Tetrapod 和 Amniote — 它们位于该路径上 — 是 Mammal 的祖先。
节点 Mammal 的后代
Bear 和 Chimpanzee 是 Mammal 的子节点。因此,它们是 Mammal 的后代。
Mammal 和 Newt 的最低共同祖先
Mammal 的祖先是 Vertebrate, Jawed Vertebrate, Tetrapod 和 Amniote。
Newt 的祖先是 Vertebrate, Jawed Vertebrate 和 Tetrapod。
在共同祖先中,层级最低(即离根最远)的是 Tetrapod。
请注意,在最低共同祖先算法中,每个节点都被视为其自身的祖先。
NetworkX 的最低共同祖先算法实现#
NetworkX 使用一种朴素算法来查找给定节点对的最低共同祖先。在本节中,我们将逐步介绍它。
步骤 1:检查输入图是否为 DAG 类型。#
NetworkX 中的最低共同祖先算法仅针对至少有一个节点的有向无环图实现。因此,源代码首先检查输入图是否有效。
def naive_all_pairs_lowest_common_ancestor(G, pairs=None):
if not nx.is_directed_acyclic_graph(G):
raise nx.NetworkXError("LCA only defined on directed acyclic graphs.")
elif len(G) == 0:
raise nx.NetworkXPointlessConcept("LCA meaningless on null graphs.")
如果未设置“pairs”参数,则默认考虑 G 中所有无序节点对,例如,我们不会同时得到 (b, a) 和 (a, b),而只得到其中一个。如果已指定 pairs,则检查 pairs 中的每个节点是否存在于输入图中。
if pairs is None:
from itertools import combinations_with_replacement
pairs = combinations_with_replacement(G, 2)
else:
pairs = dict.fromkeys(pairs)
nodeset = set(G)
for pair in pairs:
if set(pair) - nodeset:
raise nx.NodeNotFound(
f"Node(s) {set(pair) - nodeset} from pair {pair} not in G."
)
步骤 2:查找 G 中所有节点的祖先。#
完成输入验证后,我们查找 pairs 中每个节点的所有祖先,并将这些信息存储在缓存中。
ancestor_cache = {}
for v, w in pairs:
if v not in ancestor_cache:
ancestor_cache[v] = nx.ancestors(G, v)
ancestor_cache[v].add(v)
if w not in ancestor_cache:
ancestor_cache[w] = nx.ancestors(G, w)
ancestor_cache[w].add(w)
步骤 3:查找共同祖先#
对于每对 (v, w),我们确定同时出现在 \(v\) 和 \(w\) 的祖先列表中的节点。(即查找所有共同祖先)
common_ancestors = ancestor_cache[v] & ancestor_cache[w]
步骤 4:在共同祖先中查找位于图中最低层级的节点。#
我们从共同祖先集合中任意选取一个节点 \(v\)。我们沿着共同祖先集合中剩余的任意出边行进,直到到达一个没有指向其他共同祖先的出边的节点。
v = next(iter(common_ancestors))
while True:
successor = None
for w in G.successors(v):
if w in common_ancestors:
successor = w
break
if successor is None:
return v
v = successor
我们可以看到我们的算法对于一个简单的有向无环图的结果。假设我们的图 G 如下所示,我们希望找到所有节点对的最低共同祖先。为此,我们需要调用 all_pairs_lowest_common_ancestor 方法。
# Generating and visualizing our DAG
G = nx.DiGraph()
G.add_edges_from([(1, 0), (2, 0), (3, 2), (3, 1), (4, 2), (4, 3)])
pairs = combinations_with_replacement(G, 2)
pos = graphviz_layout(G, prog="dot")
plt.figure(3, figsize=(5, 3))
nx.draw(
G,
pos,
with_labels=True,
node_size=1500,
node_color="darkgreen",
font_size=14,
font_color="White",
)
plt.show()
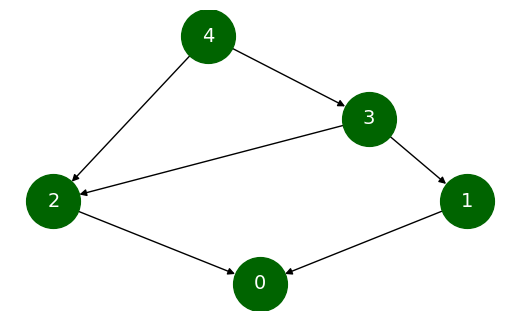
dict(nx.all_pairs_lowest_common_ancestor(G))
{(1, 1): 1,
(1, 0): 1,
(1, 2): 3,
(1, 3): 3,
(1, 4): 4,
(0, 0): 0,
(0, 2): 2,
(0, 3): 3,
(0, 4): 4,
(2, 2): 2,
(2, 3): 3,
(2, 4): 4,
(3, 3): 3,
(3, 4): 4,
(4, 4): 4}
时间与空间复杂度#
最低共同祖先算法的朴素实现会查找给定 pairs 中所有节点的祖先。设 pairs 中给定节点的数量为 P。在最坏情况下,查找单个节点的祖先需要 O(|V|) 时间,其中 |V| 是节点的数量。因此,构建图的祖先缓存需要 O(|V|*P) 时间。这一步将主导其他步骤,并决定算法的最坏情况运行时间。
算法的空间复杂度也将由祖先缓存决定。对于给定 pairs 中的每个节点,可能有 O(|V|) 个祖先。因此,空间复杂度也是 O(|V|*P)。
