有向无环图 & 拓扑排序#
在本教程中,我们将探索与有向无环图(有时称为“DAG”)相关的算法,这些算法在 NetworkX 中实现,位于 networkx/algorithms/dag.py 下。
首先,我们需要了解什么是有向图。
导入包#
import networkx as nx
import matplotlib.pyplot as plt
import inspect
%matplotlib inline
示例:有向图#
triangle_graph = nx.DiGraph([(1, 2), (2, 3), (3, 1)])
nx.draw_planar(
triangle_graph,
with_labels=True,
node_size=1000,
node_color="#ffff8f",
width=0.8,
font_size=14,
)
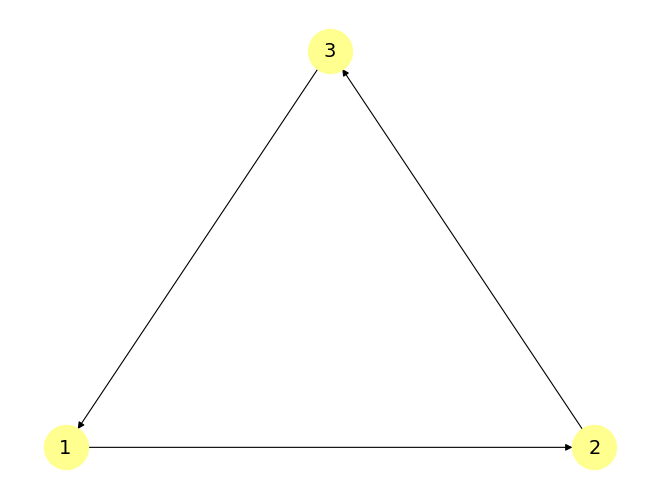
定义#
在数学,更具体地说是在图论中,有向图(或称为 DiGraph)是由一组通过有向边(通常称为弧)连接的顶点组成的图。这里的边具有方向性,这与无向图形成对比,在无向图中,边在语义上没有方向的概念。有向无环图在此基础上更进一步;通过无环,它们不包含环。您将在下面的示例中看到这个概念的应用。
有向无环图#
示例#
clothing_graph = nx.read_graphml(f"data/clothing_graph.graphml")
plt.figure(figsize=(12, 12), dpi=150)
nx.draw_planar(
clothing_graph,
arrowsize=12,
with_labels=True,
node_size=8000,
node_color="#ffff8f",
linewidths=2.0,
width=1.5,
font_size=14,
)
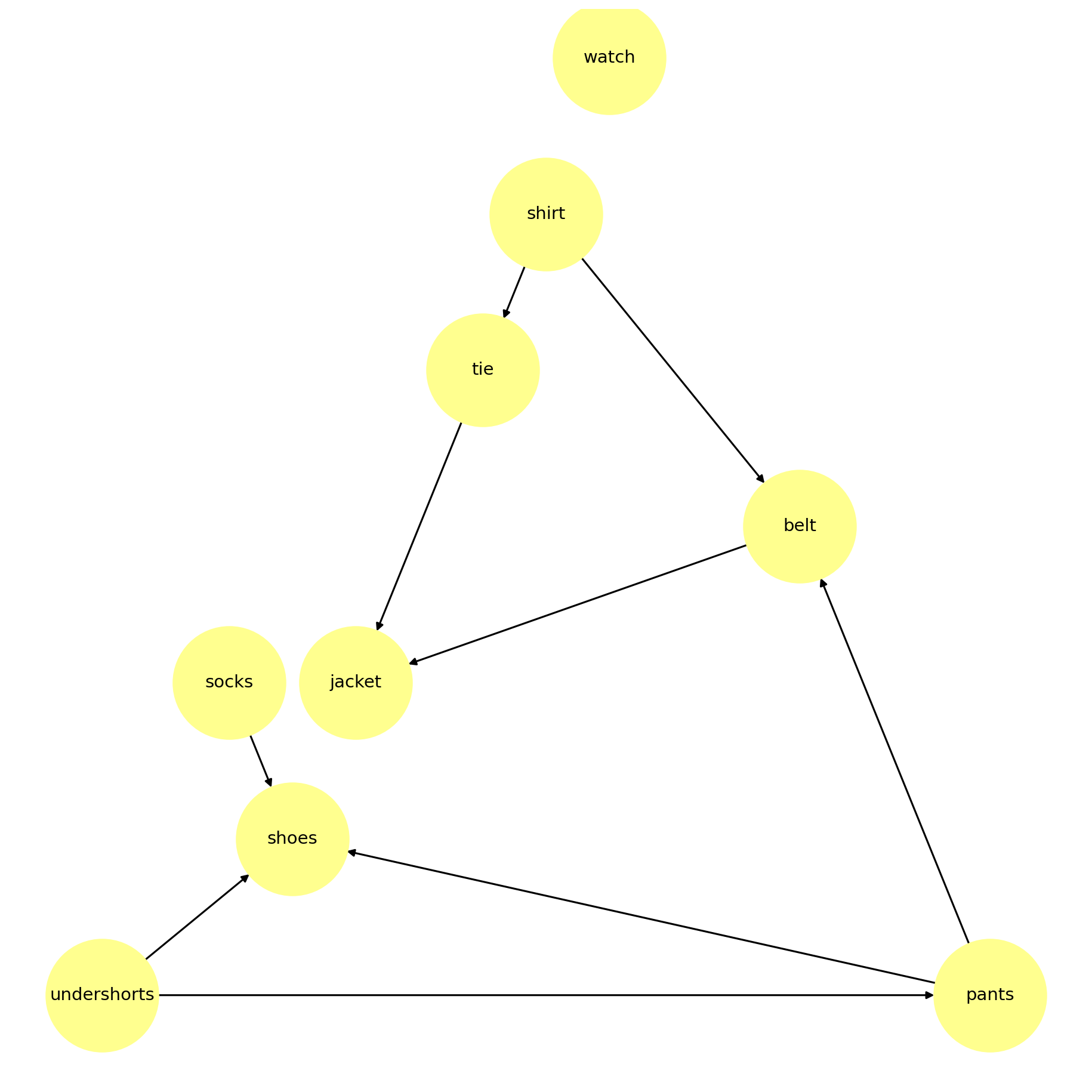
这里有一个关于 Bumstead 教授穿衣的有趣例子。根据习惯,教授会先穿某些衣服再穿其他的(例如,先穿袜子再穿鞋)。其他物品可以按任意顺序穿戴(例如,袜子和裤子)。
示例中的有向边 \((u, v)\) 表示必须先穿戴衣物 \(u\),然后才能穿戴衣物 \(v\)。
在本例中,clothing_graph 是一个 DAG。
nx.is_directed_acyclic_graph(clothing_graph)
True
相比之下,triangle_graph 不是一个 DAG。
nx.is_directed_acyclic_graph(triangle_graph)
False
这是因为 triangle_graph 包含一个环
nx.find_cycle(triangle_graph)
[(1, 2), (2, 3), (3, 1)]
应用#
有向无环图作为偏序关系的表示在具有顺序约束的任务系统调度中有着许多应用。这类问题中的一类重要问题涉及需要更新的对象集合,例如,在某个单元格更改后计算电子表格单元格的更新顺序,或者在源代码更改后识别需要更新哪些软件目标文件。在这些情境下,我们使用依赖图,它是一个图中每个需要更新的对象对应一个顶点,并且只要一个对象需要在另一个对象之前更新,就有一条边连接这两个对象。图中的环称为循环依赖,通常是不允许的,因为无法一致地调度涉及循环的任务。不含循环依赖的依赖图构成 DAG。
有向无环图也可以用来表示处理单元网络。在这种表示中,数据通过其入边进入处理单元,通过其出边离开处理单元。例如,在电子电路设计中,静态组合逻辑块可以表示为一个无环的逻辑门系统,该系统计算输入函数的输出,其中函数的输入和输出表示为单个位。
定义#
有向无环图(“DAG”或“dag”)是没有有向环的有向图。也就是说,它由顶点和边(也称为弧)组成,每条边都从一个顶点指向另一个顶点,沿着这些方向永远不会形成闭环。
有向图是 DAG 当且仅当可以通过将顶点排列成与所有边方向一致的线性顺序来对其进行拓扑排序。
拓扑排序#
现在让我们介绍一下什么是拓扑排序。
示例#
list(nx.topological_sort(clothing_graph))
['undershorts',
'shirt',
'socks',
'watch',
'pants',
'tie',
'belt',
'shoes',
'jacket']
应用#
拓扑排序的典型应用是根据依赖关系调度一系列作业或任务。作业由顶点表示,如果作业 \(u\) 必须在作业 \(v\) 开始之前完成(例如,洗衣服时,洗衣机必须完成才能将衣服放入烘干机),则存在从 \(u\) 到 \(v\) 的边。然后,拓扑排序给出了执行这些作业的顺序。
拓扑排序算法的一个密切相关应用最早在 20 世纪 60 年代早期在 PERT 技术 [1] 的背景下进行了研究,该技术用于项目管理中的调度。在此应用中,图的顶点代表项目的里程碑,边代表必须在里程碑之间执行的任务。拓扑排序是用于找到项目关键路径的线性时间算法的基础,关键路径是控制整个项目进度长度的一系列里程碑和任务。
在计算机科学中,这类应用出现在指令调度、重新计算电子表格公式值时的公式单元格求值顺序、逻辑综合、确定在 makefiles 中执行编译任务的顺序、数据序列化以及解析链接器中的符号依赖关系。它还用于决定在数据库中以外键加载表的顺序。
定义#
有向无环图 \(G = (V, E)\) 的拓扑排序是其所有顶点的线性顺序,使得如果 \(G\) 包含一条边 \((u, v)\),则在顺序中 \(u\) 出现在 \(v\) 之前。
值得注意的是,如果图包含环,则不可能进行线性排序。
将图的拓扑排序视为将其顶点沿水平线排列的顺序很有用,这样所有有向边都从左指向右。
Kahn 算法#
NetworkX 使用 Kahn 算法执行拓扑排序。这里我们将简要介绍它。
首先,找到一个“起始节点”列表,这些节点没有入边,并将它们插入集合 S 中;在一个非空无环图中,至少存在一个这样的节点。然后
L <- Empty list that will contain the sorted elements
S <- Set of all nodes with no incoming edge
while S is not empty do
remove a node N from S
add N to L
for each node M with an edge E from N to M do
remove edge E from the graph
if M has no other incoming edges then
insert M into S
if graph has edges then
return error # graph has at least one cycle
else
return L # a topologically sorted order
NetworkX 实现#
最后,让我们看看 NetworkX 中如何实现拓扑排序。
我们可以看到 Kahn 算法分层处理图,使得每一层都包含所有其依赖项已由前一层节点满足的节点。换句话说,Kahn 算法做的事情类似于
获取 DAG 中所有没有任何依赖的节点,并将它们放入列表中。
从 DAG 中“移除”这些节点。
重复此过程,每一步创建一个新列表。因此,拓扑排序被简化为以这种方式正确地对图进行分层。
这个过程在 topological_generations() 函数中实现,topological_sort() 函数基于它。
让我们逐步看看 NetworkX 中 topological_generations() 函数是如何实现的。
步骤 1. 初始化入度。#
由于 Kahn 算法中我们只关心顶点的入度,为了保留传入的图结构,我们不删除边,而是减小相应顶点的入度。因此,我们将这些值保存在一个独立的字典 indegree_map 中。
indegree_map = {v: d for v, d in G.in_degree() if d > 0}
步骤 2. 初始化第一层。#
在 Kahn 算法的每一步中,我们都会寻找入度为零的顶点。为了准备算法的第一次循环迭代,我们可以初始化一个名为 zero_indegree 的列表来存放这些节点
zero_indegree = [v for v, d in G.in_degree() if d == 0]
步骤 3. 从一层移动到下一层。#
现在,我们将展示算法如何从一层移动到下一层。
在循环内部,要考虑的第一代(this_generation)是入度为零的节点的集合。
我们处理变量 this_generation 中当前层的所有顶点,并将下一层存储在变量 zero_indegree 中。
对于 this_generation 中的每个顶点,我们移除其所有出边。
然后,如果某个顶点的入度因此变为零,则将其添加到下一层 zero_indegree,并将其从 indegree_map 字典中移除。
处理完 this_generation 中的所有节点后,我们可以生成(yield)它。
while zero_indegree:
this_generation = zero_indegree
zero_indegree = []
for node in this_generation:
for child in G.neighbors(node):
indegree_map[child] -= 1
if indegree_map[child] == 0:
zero_indegree.append(child)
del indegree_map[child]
yield this_generation
步骤 4. 检查图中是否存在环。#
如果循环完成后图中仍有顶点,则说明图中存在环,该图不是 DAG。
if indegree_map:
raise nx.NetworkXUnfeasible(
"Graph contains a cycle or graph changed during iteration"
)
补充:拓扑排序也适用于多重图。#
通过稍微修改上述算法,可以实现这一点。
首先,检查
G是否为多重图multigraph = G.is_multigraph()
然后,将
indegree_map[child] -= 1
替换为
indegree_map[child] -= len(G[node][child]) if multigraph else 1
补充:图可能在迭代过程中发生变化。#
在拓扑排序中处理不同层级之间,图可能会发生变化。我们需要在 while 循环运行时检查这一点。
要做到这一点,只需将
for node in this_generation: for child in G.neighbors(node): indegree_map[child] -= 1
替换为
for node in this_generation: if node not in G: raise RuntimeError("Graph changed during iteration") for child in G.neighbors(node): try: indegree_map[child] -= 1 except KeyError as e: raise RuntimeError("Graph changed during iteration") from e
组合所有步骤。#
将上述所有步骤结合起来,就是 NetworkX 中 topological_generations() 函数的当前实现。
print(inspect.getsource(nx.topological_generations))
@nx._dispatchable
def topological_generations(G):
"""Stratifies a DAG into generations.
A topological generation is node collection in which ancestors of a node in each
generation are guaranteed to be in a previous generation, and any descendants of
a node are guaranteed to be in a following generation. Nodes are guaranteed to
be in the earliest possible generation that they can belong to.
Parameters
----------
G : NetworkX digraph
A directed acyclic graph (DAG)
Yields
------
sets of nodes
Yields sets of nodes representing each generation.
Raises
------
NetworkXError
Generations are defined for directed graphs only. If the graph
`G` is undirected, a :exc:`NetworkXError` is raised.
NetworkXUnfeasible
If `G` is not a directed acyclic graph (DAG) no topological generations
exist and a :exc:`NetworkXUnfeasible` exception is raised. This can also
be raised if `G` is changed while the returned iterator is being processed
RuntimeError
If `G` is changed while the returned iterator is being processed.
Examples
--------
>>> DG = nx.DiGraph([(2, 1), (3, 1)])
>>> [sorted(generation) for generation in nx.topological_generations(DG)]
[[2, 3], [1]]
Notes
-----
The generation in which a node resides can also be determined by taking the
max-path-distance from the node to the farthest leaf node. That value can
be obtained with this function using `enumerate(topological_generations(G))`.
See also
--------
topological_sort
"""
if not G.is_directed():
raise nx.NetworkXError("Topological sort not defined on undirected graphs.")
multigraph = G.is_multigraph()
indegree_map = {v: d for v, d in G.in_degree() if d > 0}
zero_indegree = [v for v, d in G.in_degree() if d == 0]
while zero_indegree:
this_generation = zero_indegree
zero_indegree = []
for node in this_generation:
if node not in G:
raise RuntimeError("Graph changed during iteration")
for child in G.neighbors(node):
try:
indegree_map[child] -= len(G[node][child]) if multigraph else 1
except KeyError as err:
raise RuntimeError("Graph changed during iteration") from err
if indegree_map[child] == 0:
zero_indegree.append(child)
del indegree_map[child]
yield this_generation
if indegree_map:
raise nx.NetworkXUnfeasible(
"Graph contains a cycle or graph changed during iteration"
)
最后,让我们看看在 clothing_graph 上运行的结果。
list(nx.topological_generations(clothing_graph))
[['undershorts', 'shirt', 'socks', 'watch'],
['pants', 'tie'],
['belt', 'shoes'],
['jacket']]
