节点同配性系数和相关性度量#
在本教程中,我们将探讨同配性 [1] 的理论及其度量。
我们将重点介绍 NetworkX 中提供的同配性度量,位于 algorithms/assortativity/correlation.py
属性同配性
数值同配性
度同配性
以及与同配性度量密切相关的混合矩阵。
导入包#
import networkx as nx
import matplotlib.pyplot as plt
import pickle
import copy
import random
import warnings
%matplotlib inline
同配性#
网络中的同配性指的是节点倾向于连接其他“相似”节点而非“不相似”节点的趋势。
这里我们说两个节点在一个属性上“相似”,是指它们拥有相同的属性值。属性可以是任何结构属性,例如节点的度,也可以是其他属性,例如权重或容量。
基于这些属性,我们可以为网络提供不同的同配性度量。另一方面,我们也可以有异配性,在这种情况下,节点倾向于连接不相似的节点而不是相似的节点。
同配性系数#
假设我们有一个网络 \(N\),\(N = (V, E)\),其中 \(V\) 是网络中的节点集合,\(E\) 是网络中的边/有向边集合。此外,\(P(v)\) 表示每个节点 \(v\) 的一个属性。
混合矩阵#
设属性 \(P(v)\) 在网络中取 \(P[0],P[1],...P[k-1]\) 个不同的值,则**混合矩阵**是矩阵 \(M\),其中 \(M[i][j]\) 表示从属性为 \(P[i]\) 的节点到属性为 \(P[j]\) 的节点的边数。我们可以通过除以有序边的总数来归一化混合矩阵,即 \( e = \frac{M}{|E|}\)。
现在定义,
\(a[i]=\) 边 \((u,v)\) 中满足 \(P(u)=P[i]\) 的比例
\(b[i]=\) 边 \((u,v)\) 中满足 \(P(v)=P[i]\) 的比例
在 Python 代码中,它看起来像 a = e.sum(axis=0) 和 b = e.sum(axis=1)
最后,让 \(\sigma_a\) 和 \(\sigma_b\) 分别代表 \(\{\ P[i]\cdot a[i]\ |\ i \in 0...k-1\}\) 和 \(\{ P[i]\cdot b[i]\ |\ i \in 0...k-1\}\) 的标准差。
然后我们可以根据皮尔逊相关系数定义该属性的同配性系数。
属性同配性系数#
这里属性 \(P(v)\) 是分配给每个名义节点的属性。如上所述,我们计算归一化混合矩阵 \(e\),并由此定义属性同配性系数 [2] 如下。
从现在开始,我们将使用下标表示法来表示索引,例如 \(P_i = P[i]\) 和 \(e_{ij} = e[i][j]\)
它通过 attribute_assortativity_coefficient 实现。
数值同配性系数#
这里属性 \(P(v)\) 是分配给每个节点的数值属性,归一化混合矩阵 \(e\),\(\sigma_a\) 和 \(\sigma_b\) 的定义与上文相同。由此我们定义数值同配性系数 [2] 如下。
它通过 numeric_assortativity_coefficient 实现。
度同配性系数#
对于有向网络的度同配性测量,与属性同配性相比,我们有更多选项,因为我们有两种类型的度,即入度和出度。基于这两种类型的度,我们可以测量 \(2 \times 2 =4\) 种不同类型的度同配性 [3]
r(in,in):衡量存在有向边 (u,v) 且入度(u) = 入度(v) 的趋势。
r(in,out):衡量存在有向边 (u,v) 且入度(u) = 出度(v) 的趋势。
r(out,in):衡量存在有向边 (u,v) 且出度(u) = 入度(v) 的趋势。
r(out,out):衡量存在有向边 (u,v) 且出度(u) = 出度(v) 的趋势。
注意:如果网络是无向的,则所有这 4 种类型的度同配性是相同的。
为了定义所有 4 种类型的度同配性系数,我们需要对 \(P[i]\) 和 \(e\) 的定义进行微小修改,而 \(\sigma_a\) 和 \(\sigma_b\) 的定义保持不变。
设 \(x,y \in \{in,out\}\)。属性 \(P(\cdot)\) 取自 \(x\)-度\((\cdot)\) 和 \(y\)-度\((\cdot)\) 所取值的并集中的不同值,而 \(e_{i,j}\) 是有向边 \((u,v)\) 中满足 \(x\)-度\((u) = P_i\) 和 \(y\)-度\((v) = P_j\) 的比例。
它通过 degree_assortativity_coefficient 和 degree_pearson_correlation_coefficient 实现。后一个函数使用 scipy.stats.pearsonr 计算同配性系数,这可能使其更快。
同配性示例#
说明同配性值的变化方式
gname = "g2"
G = nx.read_graphml(f"data/{gname}.graphml")
with open(f"data/pos_{gname}", "rb") as fp:
pos = pickle.load(fp)
fig, axes = plt.subplots(4, 2, figsize=(20, 20))
# assign colors and labels to nodes based on their 'cluster' and 'num_prop' property
node_colors = ["orange" if G.nodes[u]["cluster"] == "K5" else "cyan" for u in G.nodes]
node_labels = {u: G.nodes[u]["num_prop"] for u in G.nodes}
for i in range(8):
g = nx.read_graphml(f"data/{gname}_{i}.graphml")
# calculating the assortativity coefficients wrt different proeprties
cr = nx.attribute_assortativity_coefficient(g, "cluster")
r_in_out = nx.degree_assortativity_coefficient(g, x="in", y="out")
nr = nx.numeric_assortativity_coefficient(g, "num_prop")
# drawing the network
nx.draw_networkx_nodes(
g, pos=pos, node_size=300, ax=axes[i // 2][i % 2], node_color=node_colors
)
nx.draw_networkx_labels(g, pos=pos, labels=node_labels, ax=axes[i // 2][i % 2])
nx.draw_networkx_edges(g, pos=pos, ax=axes[i // 2][i % 2], edge_color="0.7")
axes[i // 2][i % 2].set_title(
f"Attribute assortativity coefficient = {cr:.3}\nNumeric assortativity coefficient = {nr:.3}\nr(in,out) = {r_in_out:.3}",
size=15,
)
fig.tight_layout()
/home/circleci/repo/venv/lib/python3.12/site-packages/networkx/algorithms/assortativity/correlation.py:302: RuntimeWarning: invalid value encountered in scalar divide
return float((xy * (M - ab)).sum() / np.sqrt(vara * varb))
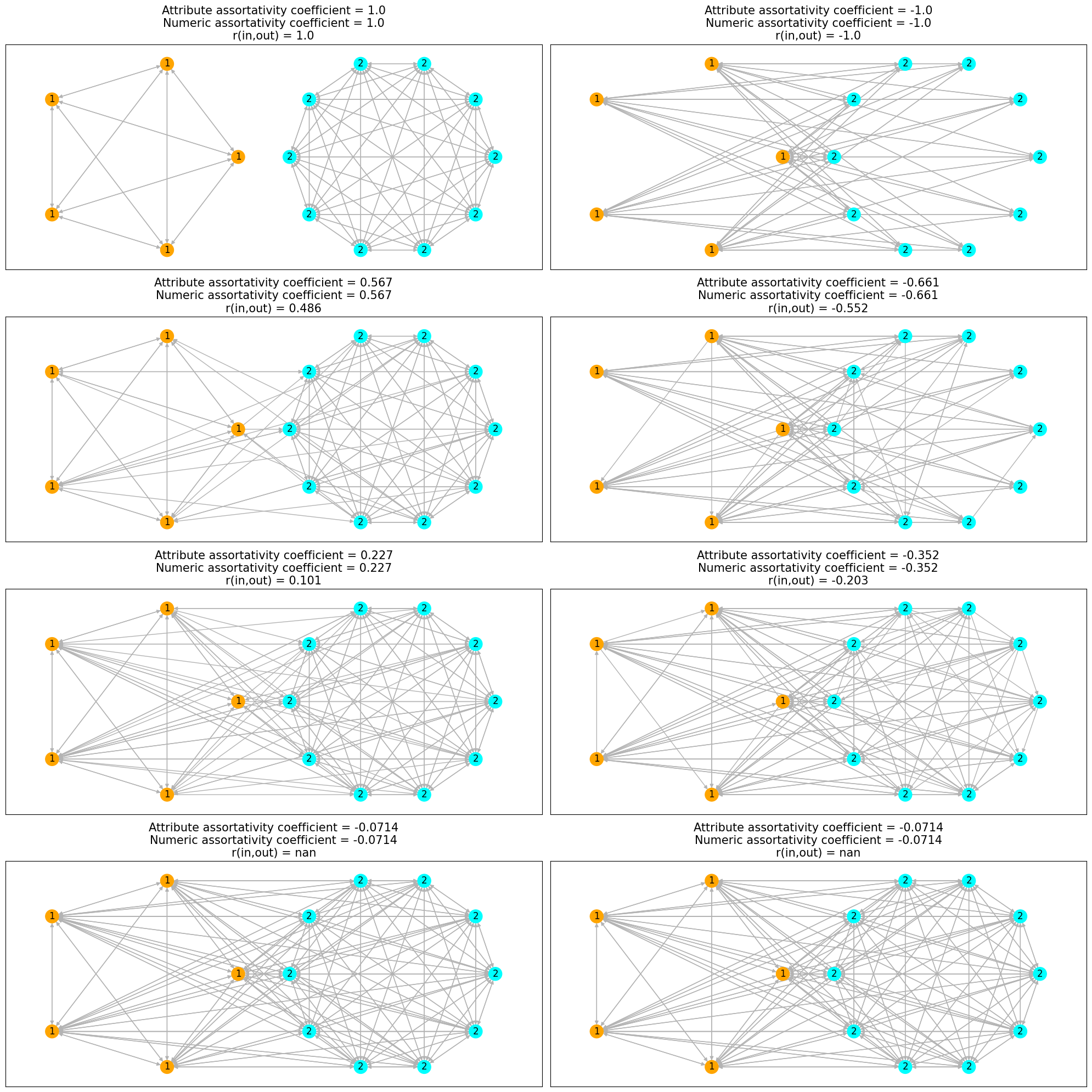
节点根据 cluster 属性着色,并根据 num_prop 属性标记。我们可以观察到,左侧的初始网络是完全同配的,而右侧的其补图是完全异配的。随着我们在同配(异配)网络中添加具有不同(相似)属性的节点之间的边,网络趋向于非同配网络,并且两个同配性系数的值都趋向于 \(0\)。
在 attribute_assortativity_coefficient 和 numeric_assortativity_coefficient 中的参数 nodes 指定了哪些节点的边将被考虑用于计算混合矩阵。也就是说,如果 \((u,v)\) 是一条有向边,则当 \(u\) 在 nodes 中时,边 \((u,v)\) 将被用于计算混合矩阵。对于无向情况,如果 \(u\) 或 \(v\) 中至少有一个在 nodes 中,则考虑该边。
在 degree_assortativity_coefficient 和 degree_pearson_correlation_coefficient 中,nodes 参数的解释不同,它指定了构成一个子图的节点,这些子图的边将被考虑用于计算混合矩阵。
# list of nodes to consider for the i'th network in the example
# Note: passing 'None' means to consider all the nodes
nodes_list = [
None,
[str(i) for i in range(3)],
[str(i) for i in range(4)],
[str(i) for i in range(5)],
[str(i) for i in range(4, 8)],
[str(i) for i in range(5, 10)],
]
fig, axes = plt.subplots(3, 2, figsize=(20, 16))
def color_node(u, nodes):
"""Utility function to give the color of a node based on its attribute"""
if u not in nodes:
return "0.85"
if G.nodes[u]["cluster"] == "K5":
return "orange"
else:
return "cyan"
# adding a edge to show edge cases
G.add_edge("4", "5")
for nodes, ax in zip(nodes_list, axes.ravel()):
# calculating the value of assortativity
cr = nx.attribute_assortativity_coefficient(G, "cluster", nodes=nodes)
nr = nx.numeric_assortativity_coefficient(G, "num_prop", nodes=nodes)
# drawing network
ax.set_title(
f"Attribute assortativity coefficient: {cr:.3}\nNumeric assortativity coefficient: {nr:.3}\nNodes = {nodes}",
size=15,
)
if nodes is None:
nodes = [u for u in G.nodes()]
node_colors = [color_node(u, nodes) for u in G.nodes]
nx.draw_networkx_nodes(G, pos=pos, node_size=450, ax=ax, node_color=node_colors)
nx.draw_networkx_labels(G, pos, labels={u: u for u in G.nodes}, font_size=15, ax=ax)
nx.draw_networkx_edges(
G,
pos=pos,
edgelist=[(u, v) for u, v in G.edges if u in nodes],
ax=ax,
edge_color="0.3",
)
fig.tight_layout()
/home/circleci/repo/venv/lib/python3.12/site-packages/networkx/algorithms/assortativity/correlation.py:282: RuntimeWarning: invalid value encountered in scalar divide
r = (t - s) / (1 - s)
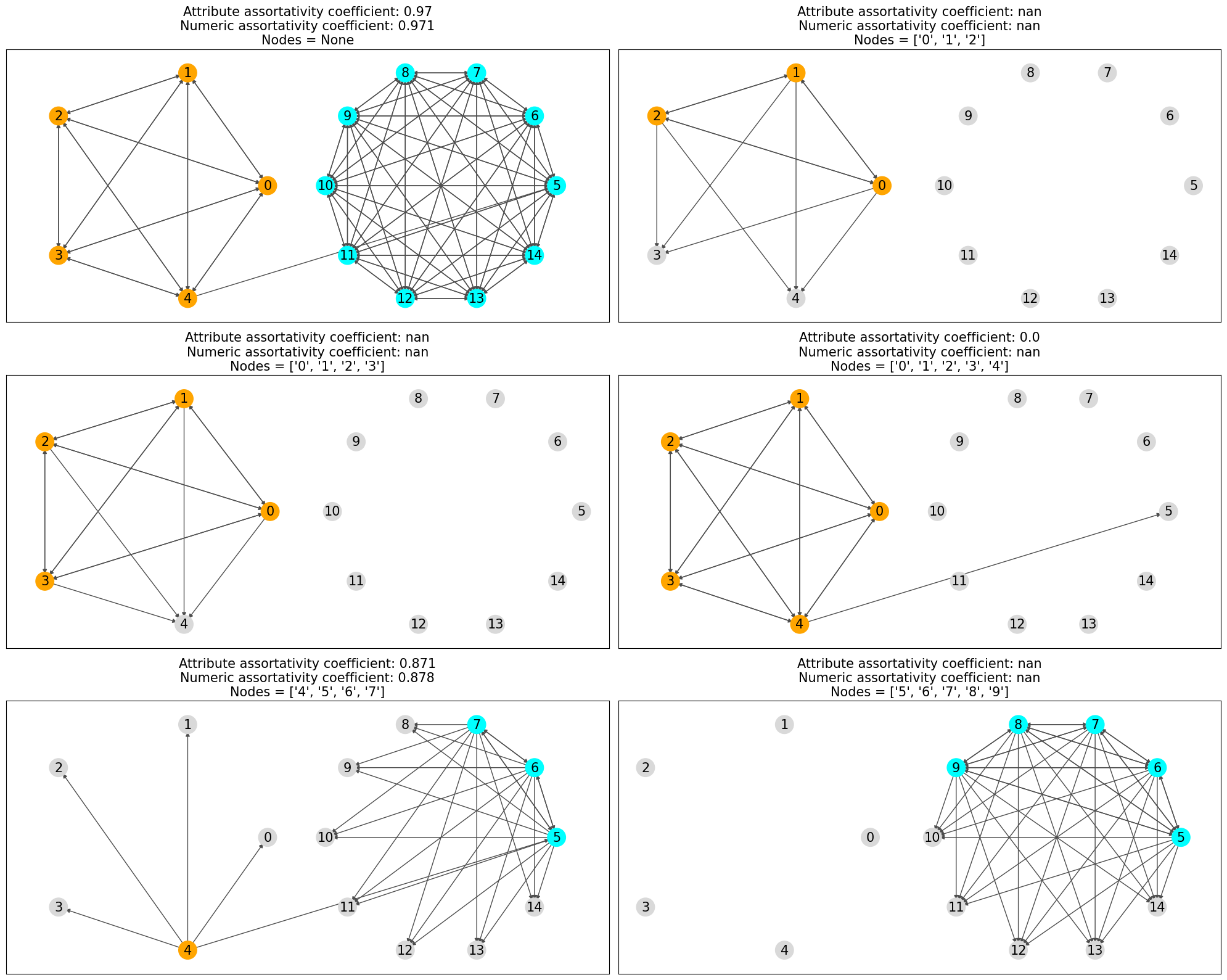
在上述图中,只有被考虑的节点被着色,其余节点被灰显,并且只绘制了在同配性计算中被考虑的边。
