旅行商问题

这是一个旅行商问题的绘图解法示例

用于生成解法的函数是 christofides，它可以在给定一组节点的情况下，计算出旅行者为最小化总成本必须遵循的节点路线。

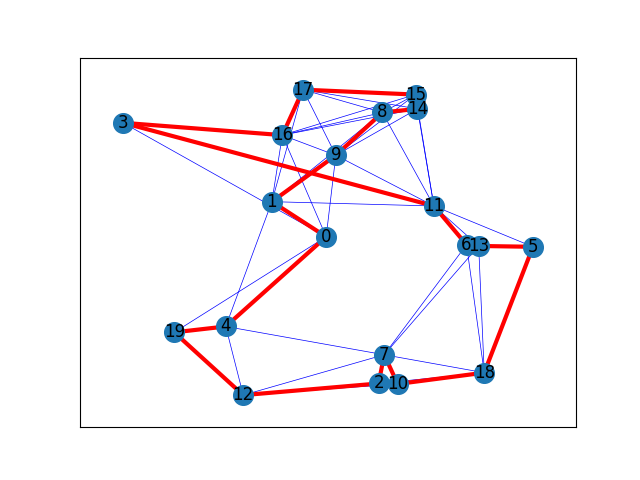
The route of the traveller is: [0, 4, 19, 12, 2, 7, 10, 18, 5, 13, 6, 11, 3, 16, 17, 15, 14, 8, 9, 1, 0]

import matplotlib.pyplot as plt
import networkx as nx
import networkx.algorithms.approximation as nx_app
import math

G = nx.random_geometric_graph(20, radius=0.4, seed=3)
pos = nx.get_node_attributes(G, "pos")

# Depot should be at (0,0)
pos[0] = (0.5, 0.5)

H = G.copy()


# Calculating the distances between the nodes as edge's weight.
for i in range(len(pos)):
    for j in range(i + 1, len(pos)):
        dist = math.hypot(pos[i][0] - pos[j][0], pos[i][1] - pos[j][1])
        dist = dist
        G.add_edge(i, j, weight=dist)

cycle = nx_app.christofides(G, weight="weight")
edge_list = list(nx.utils.pairwise(cycle))

# Draw closest edges on each node only
nx.draw_networkx_edges(H, pos, edge_color="blue", width=0.5)

# Draw the route
nx.draw_networkx(
    G,
    pos,
    with_labels=True,
    edgelist=edge_list,
    edge_color="red",
    node_size=200,
    width=3,
)

print("The route of the traveller is:", cycle)
plt.show()