引言#

NetworkX 的结构可以从其源代码的组织方式中看出。该软件包提供了用于图对象的类、创建标准图的生成器、读取现有数据集的 IO 例程、分析结果网络的算法以及一些基本的绘图工具。

NetworkX API 的大部分功能由接受图对象作为参数的函数提供。图对象的方法仅限于基本操作和报告。这提供了代码和文档的模块化。这也使新手更容易逐步学习软件包。每个模块的源代码都易于阅读，阅读这些 Python 代码实际上是学习更多网络算法的好方法，但我们也投入了大量精力使文档内容充分且友好。如果您有建议或问题，请加入 NetworkX Google 群组 与我们联系。

类的命名使用 CamelCase（每个单词的首字母大写）。函数、方法和变量名使用 lower_case_underscore（小写，单词之间用下划线分隔）。

NetworkX 基础#

启动 Python 后，使用（推荐方式）导入 networkx 模块

import networkx as nx

为了避免重复，在文档中我们假定 NetworkX 已通过此方式导入。

如果导入 networkx 失败，这意味着 Python 找不到已安装的模块。请检查您的安装和您的 PYTHONPATH。

以下基本图类型作为 Python 类提供

Graph

  • 此类实现无向图。它忽略两个节点之间的多条边。它允许节点与自身之间的自环边。

DiGraph

  • 有向图，即带有有向边的图。提供有向图共有的操作（是 Graph 的子类）。

MultiGraph

  • 一种灵活的图类，允许节点对之间有多条无向边。额外的灵活性会导致性能有所下降，尽管通常不显著。

MultiDiGraph

  • MultiGraph 的有向版本。

空的类图对象使用以下方式创建

G = nx.Graph()
G = nx.DiGraph()
G = nx.MultiGraph()
G = nx.MultiDiGraph()

所有图类都允许任何 可哈希 (hashable) 对象作为节点。可哈希对象包括字符串、元组、整数等。任意边属性（如权重和标签）可以与边关联。

图的内部数据结构基于邻接表表示，并使用 Python 字典 数据结构实现。图的邻接结构被实现为一个字典的字典；外部字典以节点为键，对应的值本身是字典，这些内部字典以相邻节点为键，指向与该边关联的边属性。这种“字典的字典”结构允许在大图中快速添加、删除和查找节点和邻居。底层数据结构由类定义中的方法（编程接口“API”）直接访问。另一方面，所有函数都完全通过这些 API 方法操作类图对象，而不是直接操作数据结构。这种设计允许将来用实现相同方法的替代数据结构替换基于“字典的字典”的数据结构。

图#

使用 NetworkX 时要做的第一个选择是使用哪种类型的图对象。图（网络）是节点的集合以及边的集合，边是节点对。属性通常与节点和/或边关联。NetworkX 图对象根据网络的两个主要属性提供不同的类型

  • 有向：边是有向的吗？边对 \((u, v)\) 的顺序重要吗？有向图通过类名中的“Di”前缀指定，例如 DiGraph。我们做出这种区分是因为许多经典的图属性对有向图的定义不同。

  • 多重边：每对节点之间允许多条边吗？正如您可能想象的，多重边需要不同的数据结构，尽管聪明的用户可以设计边数据属性来支持此功能。我们为这种类型的图提供了一种标准的数据结构和接口，使用“Multi”前缀，例如 MultiGraph。

基本的图类命名为：Graph, DiGraph, MultiGraph, 和 MultiDiGraph

节点和边#

在指定图时，您必须做的下一个选择是使用哪种类型的节点和边。

如果您只关心网络的拓扑结构，那么使用整数或字符串作为节点是合理的，并且您无需担心边数据。如果您已经有一个数据结构来描述节点，只要它是 可哈希 (hashable) 的，您可以直接使用该结构作为节点。如果它不可哈希，您可以使用唯一标识符来表示节点，并将数据作为 节点属性 (node attribute) 分配。

边通常有关联的数据。任意数据可以作为 边属性 (edge attribute) 与边关联。如果数据是数字的，并且目的是表示一个 加权图 (weighted graph)，那么请对属性使用‘weight’关键字。一些图算法，例如 Dijkstra 最短路径算法，默认使用此属性名称来获取每条边的权重。

在添加边时，可以使用 关键字/值 对将属性分配给边。您可以使用任何关键字来命名您的属性，然后使用该属性关键字查询边数据。

一旦您决定了如何编码节点和边，以及您是使用带有或不带多重边的无向图/有向图，您就可以开始构建您的网络了。

图的创建#

NetworkX 图对象可以通过以下三种方式之一创建

  • 图生成器——创建网络拓扑结构的标准算法。

  • 从预先存在的（通常是文件）源导入数据。

  • 显式添加边和节点。

显式添加和删除节点/边是最容易描述的。每个图对象都提供了操作图的方法。例如，

G = nx.Graph()
G.add_edge(1, 2)  # default edge data=1
G.add_edge(2, 3, weight=0.9)  # specify edge data

边属性可以是任何东西

import math
G.add_edge('y', 'x', function=math.cos)
G.add_node(math.cos)  # any hashable can be a node

您可以一次添加多条边

elist = [(1, 2), (2, 3), (1, 4), (4, 2)]
G.add_edges_from(elist)
elist = [('a', 'b', 5.0), ('b', 'c', 3.0), ('a', 'c', 1.0), ('c', 'd', 7.3)]
G.add_weighted_edges_from(elist)

有关更多示例，请参阅 教程。

一些基本的图操作，例如并集和交集，在 operators module 文档中描述。

图生成器，例如 binomial_graph() 和 erdos_renyi_graph()，在 graph generators 子包中提供。

要从 GML、GraphML、边列表文本文件等格式导入网络数据，请参阅 reading and writing graphs 子包。

图的报告#

类视图 (Class views) 提供节点、邻居、边和度的基本报告。这些视图提供了对属性的迭代以及成员查询和数据属性查找。这些视图引用图的数据结构，因此对图的更改会反映在视图中。这类似于 Python 3 中的字典视图。如果您想在迭代时更改图，则需要使用例如 for e in list(G.edges):。这些视图提供了集合式操作 (set-like operations)，例如并集和交集，以及使用 G.edges[u, v]['color'] 和 for e, datadict in G.edges.items(): 进行的字典式查找 (dict-like lookup) 和数据属性迭代。方法 G.edges.items() 和 G.edges.values() 与 Python 字典中的方法类似。此外，G.edges.data() 提供了特定的属性迭代，例如 for e, e_color in G.edges.data('color'):。

边的基本图关系可以通过两种方式获取。一种是查找节点的邻居，另一种是查找边。我们开玩笑地将关注节点/邻居的人称为“节点中心论者 (node-centric)”，将关注边的人称为“边中心论者 (edge-centric)”。NetworkX 的设计者倾向于节点中心，将边视为节点之间的关系。这可以从我们选择的查找表示法中看出，例如 G[u] 提供邻居（邻接），而边查找是 G.edges[u, v]。大多数稀疏图的数据结构本质上是邻接列表，因此符合这种观点。当然，最终以哪种方式检查图并不重要。G.edges 会移除无向边的重复表示，而跨所有节点的邻居报告自然会报告两个方向。

任何比边、邻居和度更复杂的属性都由函数提供。例如，nx.triangles(G, n) 返回包含节点 n 作为顶点的三角形数量。这些函数在代码和文档中归类在 算法 (algorithms) 术语下。

算法#

NetworkX 提供了许多图算法。这些包括 最短路径 (shortest path)、和 广度优先搜索 (breadth first search)（请参阅 traversal）、聚类和同构算法等。还有很多我们尚未开发的算法。如果您实现了对他人有用的图算法，请通过 NetworkX Google 群组 或 GitHub 开发者专区 告知我们。

例如，以下是使用 Dijkstra 算法查找最短加权路径的代码

G = nx.Graph()
e = [('a', 'b', 0.3), ('b', 'c', 0.9), ('a', 'c', 0.5), ('c', 'd', 1.2)]
G.add_weighted_edges_from(e)
print(nx.dijkstra_path(G, 'a', 'd'))

['a', 'c', 'd']

绘制#

虽然 NetworkX 的设计目的不是作为网络绘图工具，但我们提供了与绘图软件包和一些简单布局算法的简单接口。我们通过（建议的）pygraphviz 包或 pydot 接口与优秀的 Graphviz 布局工具（如 dot 和 neato）对接。绘图可以使用外部程序或 Matplotlib Python 包完成。交互式 GUI 界面是可能的，但未提供。绘图工具在 drawing 模块中提供。

基本的绘图函数本质上是使用您通过字典提供的节点位置或使用布局函数计算的位置将节点放置在散点图上。边是这些点之间的连线。

import matplotlib.pyplot as plt
G = nx.cubical_graph()
subax1 = plt.subplot(121)
nx.draw(G)   # default spring_layout
subax2 = plt.subplot(122)
nx.draw(G, pos=nx.circular_layout(G), node_color='r', edge_color='b')
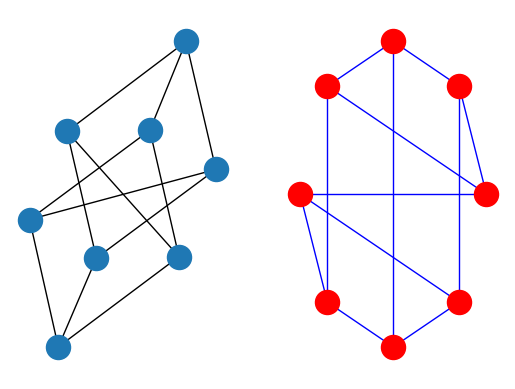
../_images/94c232c7aafe07eab83385ae4d74c33dc1341ff3a7004766a43444e935e60e2c.png

有关更多想法，请参阅 examples。

数据结构#

NetworkX 使用“字典的字典的字典”作为基本的网络数据结构。这使得对于大型稀疏网络能够实现快速查找和合理的存储。键是节点，因此 G[u] 返回一个以邻居为键指向边属性字典的邻接字典。dict 式对象 G.adj 提供邻接数据结构的视图，例如 for node, nbrsdict in G.adj.items():。表达式 G[u][v] 返回边属性字典本身。使用字典的值为列表也是可能的，但这样既不能快速检测边，也不方便存储边数据。

字典的字典的字典数据结构的优点

  • 通过两次字典查找找到并移除边。

  • 优先于“列表”，因为稀疏存储时查找速度快。

  • 优先于“集合”，因为数据可以附加到边上。

  • G[u][v] 返回边属性字典。

  • n in G 测试节点 n 是否在图 G 中。

  • for n in G: 迭代遍历图。

  • for nbr in G[n]: 迭代遍历邻居。

例如，以下是具有边 \((A, B)\) 和 \((B, C)\) 的无向图的表示。

G = nx.Graph()
G.add_edge('A', 'B')
G.add_edge('B', 'C')
print(G.adj)

{'A': {'B': {}}, 'B': {'A': {}, 'C': {}}, 'C': {'B': {}}}

对于每个基本图类，数据结构都会略有变化。对于 DiGraph，提供了两个字典的字典的字典结构，一个用于 后继 (successors) (G.succ)，一个用于 前驱 (predecessors) (G.pred)。对于 MultiGraph/MultiDiGraph，我们使用一个字典的字典的字典的字典 [1]，其中第三个字典以边键标识符为键，指向包含该边在两个节点之间属性的第四个字典。

图提供了访问边数据属性的两种接口：adjacency 和 edges。因此，G[u][v]['width'] 与 G.edges[u, v]['width'] 相同。

G = nx.Graph()
G.add_edge(1, 2, color='red', weight=0.84, size=300)
print(G[1][2]['size'])
print(G.edges[1, 2]['color'])

300
red

脚注

本页内容